2022-01-27 / Ahn Louise
In this article we introduce formulas which in simple linear process flows can be used to estimate cycle time from variability and capacity utilisation in the processes. A more detailed presentation can be found in [Hopp & Spearman] (see references at the bottom).
Little’s Law
The first of the process flow formulas is called Little’s law. It provides a fundamental relation from cycle time (CT) and throughput (TH) to work-in-process (WIP):
(1) ![]()
The law simply states that the average amount of work in the system equals the average output multiplied by average time in the system.
The equation works on averages, so over a shorter period of time, the Little’s law may not apply. This is especially true in periods of ramp-up or ramp-down.
Propagation of Variability
In a process flow, when one process succeeds other processes, the arrival variability is dependent on the departure variability of the previous processes. In the simplest situation where process ![]() immediately follow process
immediately follow process ![]() , and all jobs from process
, and all jobs from process ![]() move to process
move to process ![]() , and process
, and process ![]() is not dependent on any other processes, then the arrival rate
is not dependent on any other processes, then the arrival rate ![]() and arrival variability (CV)
and arrival variability (CV) ![]() of process
of process ![]() equal the departure rate
equal the departure rate ![]() and departure variability
and departure variability ![]() of process
of process ![]() , respectively:
, respectively:
![]()
Assuming there is no loss in process ![]() , the departure rate equals the arrival rate, but the departure variability is highly dependent also on the utilisation
, the departure rate equals the arrival rate, but the departure variability is highly dependent also on the utilisation ![]() and the process time variability given by
and the process time variability given by ![]() , the CV of the effective process time distribution.
, the CV of the effective process time distribution.
[Hopp & Spearman] provides the following estimate of ![]() for a process at a workstation having
for a process at a workstation having ![]() identical machines with reference to [Buzacott & Shanthikumar]:
identical machines with reference to [Buzacott & Shanthikumar]:
(2) ![]()
For one machine, the equation reduces to
(3) ![]()
The last formula supports the intuition that if utilisation high and the workstation is always busy, i.e. ![]() , then departure variability equals process time variability
, then departure variability equals process time variability ![]() , while if utilisation is very low, the departure variability is highly correlated with arrival variability.
, while if utilisation is very low, the departure variability is highly correlated with arrival variability.
Impact on Cycle Time – Queueing
Now, the amount of variability in itself is not that interesting. What matters is how the variability affects cycle time.
To understand this, mathematical queueing theory is applied.
[Hopp & Spearman] presents this formula for calculation of the average queue time ![]() before a process with
before a process with ![]() identical machines at utilisation
identical machines at utilisation ![]() :
:
(4) 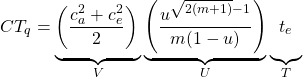
Here
[Hopp & Spearman] uses the descriptive name ‘the VUT equation’ for equation (4), where VUT is short for ‘Variability-Utilisation-Time’ since the equation can be seen as having a variability term ![]() , a utilisation term
, a utilisation term ![]() and a time term
and a time term ![]() .
.
Calculating the total cycle time is now trivial given the effective process time ![]() :
:
(5) ![]()
Example of Calculations
In this Excel sheet I have implemented the calculations for a three step process with single machines. Try it out to get an intuition of how different levels of variability and utilisation affect cycle time.
References
- John A. Buzacott & J. George Shanthikumar: “Stochastic Models of Manufacturing Systems”, Prentice Hall, 1993
- Wallace J. Hopp & Mark L. Spearman: “Factory Physics”, 2nd ed., McGraw-Hill, 2000